Batteries
A battery contains one or more elechtrochemical cells in which chemical reactions create an electrical potential between two immersed terminals. This potential can be discharged as current passing through a load.
Current
The current delivered by a battery will be largely determined by the resistance of the external load placed between its terminals, as well as the internal resistance of the battery. This should be thought of as an active part of the circuit. Since a battery will deliver no current if there is no load, current must be measured while a load is attached, and cannot be measured by a meter alone. Current must always be measured with the meter in series with the load, and the polarity of the meter must correspond with the polarity of the battery.
Capacity
The electrical capacity of a battery is measured in amp-hours (Ah), smaller values in milliamp-hours (mAh). If I is the current being drawn from a battery (in amps) and T is the time for which the battery can deliver that current (in hours), the amp-hour capacity is given by the formula:
Ah = I * T
By turning the formula around, if we know the amp-hour rating, we can calculate the time in hours for which a battery can deliver a particular current:
T = Ah / I
Theoretically, Ah is a constant value for any given battery. Thus a battery rated for 4 Ah should provide 1 amp for 4 hours, 4 amps for 1 hour, 5 amps for 0.8 hours (48 min.), and so on. In reality, this linear relationship does not exist. It quickly breaks down as the current rises. Some of the current is lost at heat, and the battery may be electrochemically incapable of keeping up with demand.
The Peukert number is a fudge factor to obtain a more realistic value for T at higher currents. If nis the Peukert number for a perticular battery, then the previous formula can be modified thus:
T = Ah / In
Manufacturers usually supply Peukert's number in their specification for a battery. If a battery has been rated at 4 Ah, and its Peukert number is 1.2, and I = 5 (ie. we want to know for how long a time, T, the battery can deliver 5 amps):
T = 4 / 51.2 = approx. 4 / 6.9, about 0.58 hours (35 min.)
More modern formulas has been revised to take into account the way in which Ah ratings are established by manufaturers today. Suppose that AhM is the modern rating for the battery's capacity in amp-hours, H is the duration in hours for which the battery was tested when the manufacturer calibrated it, n is Peukert's number (supplied by the manufacturer), and I is the current you hope to draw from the battery. This is the revised formula to determine T:
T = H * (AhM / (I * H)n)
The value of H is often supplied in the battery specification. The term C-rate are sometimes used as an alternative, which can be defined as 1/H. This means you can easily get the value for H if you know the C-rate:
H = 1 / C-rate
We can the use the revised formula to rework the original calculation. If the battery was rated for 4 Ah using the modern system, in a discharge test that lasted 20 hours (which is the same as a C-rate of 0.05), and the manufacturer still states that it has a Peukert number of 1.2, and we want to know for how long we can draw 5 A from it:
T = 20 * (4 / (5 * 20)1.2) = approx. 20 * 0.021, about 0.42 hours (25 min.)
One additional factor: For any rechargable battery, the Peukert number gradually increases with age, as the battery deteriorates chemically.
Voltage
The rated voltage of a fully charged battery is known as the open circuit voltage (OCV or VOC), defined as the potential that exists when no load is imposed between the terminals. A multimeter can be connected directly between the battery terminals with no load present due to the internal resistance of the volt meter. The meter will show the OCV quite accurately. A fully charged 12 V battery may have an OCV of about 12.6 V, while a fresh 9 V alkaline battery typically has an OCV of about 9.5 V.
The voltage delivered by a battery will be pulled down significantly when a load is applied to it, and will decrease further as time passes during a discharge cycle. For this reason, a voltage regulator is required when a battery powers components such as digital integrated circuit chips, which do not tolerate a wide variation in voltage.
To measure voltage while a load is applied to the battery, the meter must be connected in parallel with the load. This type of measurement will give a reasonably accurate reading for the potential applied to the load.
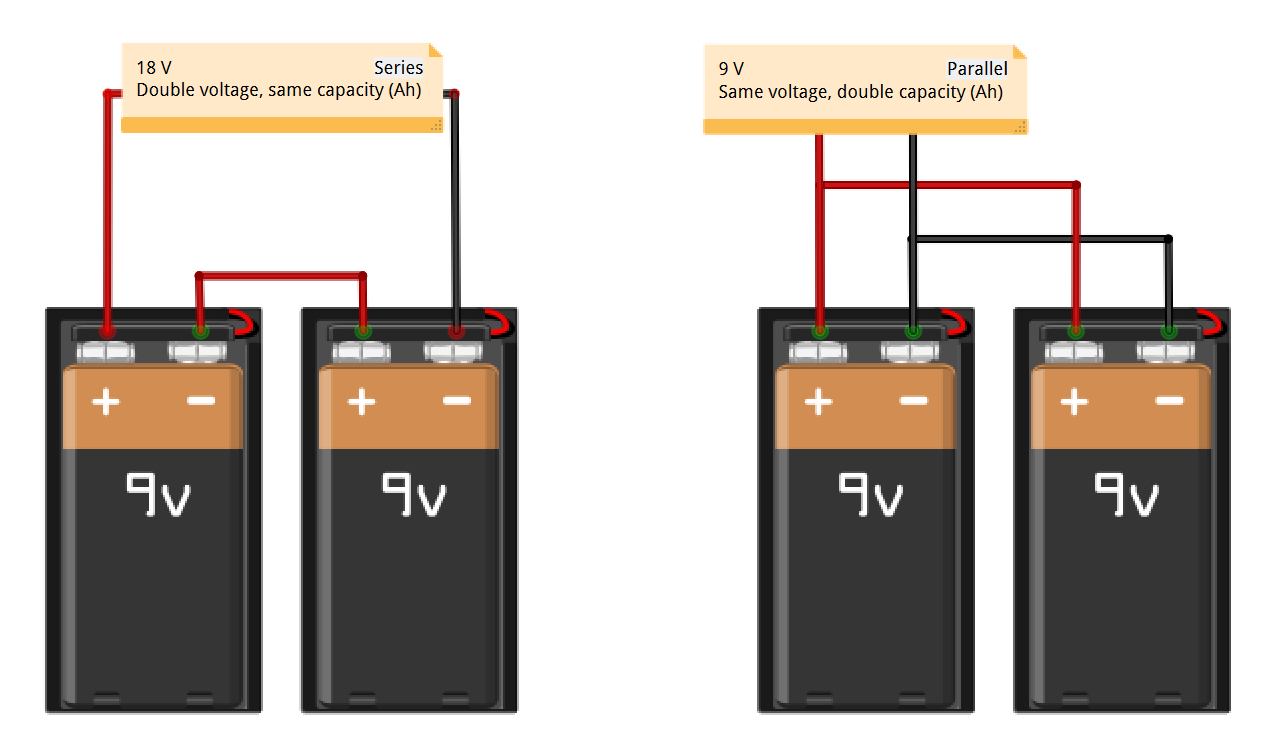
Series vs. parallel
Batteries may be used in series or in parallel. In series, the total voltage of the cain of cells is found by summing their individual voltages, while their amp-hour rating remains the same. Wired in parallel, the total voltage remains the same as for a single cell, while the combined amp-hour value is found by summing their individual amp-hour ratings.